"Musiqi dünyası" № 1 (70) 2017

Article №1; 7722 - 7754 pр.
Violetta Yunusova, Alexander Kharuto. Computer Sound Analysis of Traditional Music of Asia¹
Text PDF

Musical sound is an objective representation of written score or of some ‘ideal’ text which is ‘stored’ in the mind of traditional musicians. This sound will be percept by human hearing; on the other hand, it can be measured objectively with help of physical methods. Since the last quarter of XX century, computer-aid research in ethnomusicology becomes more and more popular. It supplements the existing ‘traditional’ methods and allows to get objective sound parameters and to derive important musicological information.

In general, following objects of ethnomusicology can be studied with help of computers:

musical sound itself — analysis of sound spectrum structure, exact sound pitch, or uncertain sound pitch, sound duration;

musical instruments — exact sound pitch row, spectrum characteristics, sound attack and decay parameters;

instrumental music — solo and ensemble sounding;

vocal techniques and traditional singing styles, it’s objective properties — spectrum parameters, formants;

structure of musical piece — parameters of melody line, sound pitch row and it’s properties (zones of tones condensation, interval system), timbre and its models (formants, harmonics);

general parameters of musical language, including sound pitch system, timbre properties, musical harmony, rhythm and tempo, and agogics.

The article deals with computer sound investiga-tions of traditional Asian music, fulfilled within more than twenty years in the Moscow P. I. Tchaikovsky Conservatory. The main directions of this computer-aid study are: analysis of sound spectrum structure and parameters (timbre), exact melody extraction and analysis of its elements and used pitch row, analysis of some properties of performing style. (Our computer investigations do not envelope all the possible items listed above.) The analysis has been fulfilled with help of programme SPAX especially developed by one of the authors (A. Kharuto, 2005) during last 20 years — from the first set of programs in 1996 (MS DOS) until now (a demo-version for Windows is available on www.kharuto.ru).

Computer analysis represented in the article was made for examples of professional music of oral tradition, collected by one of the authors (V. Yunusova) during 1979–2009 years in Azerbaijan and Central Asia and video- and audio-recordings of traditional musicians’ performances in Moscow in 2012–2015, and also for samples of Kazakhstan professional music of oral tradition from S. Utegalieva’s archive. The using of uneven-tempered 17-stage system by traditional musicians, specifics of its perception by these musicians and also by ethnomusicologists, parameters of voice timbre characteristics have been discussed by one of the authors (V. Yunusova) with native tradition bearers.

Short history

For a long time, sound properties could be estimated only with the hearing. In the middle of XIX century, first investigations of tone perception have been made by H. Helmholtz with help of tuned cavity resonators (Helmholtz, 1863). He also explained the effect of consonance sounding based on overtone interaction and calculated the consonance curve for pairs of tones.

Study of traditional musical cultures of different people around the world showed that they use different sound pitch rows, which do not match with the 12-halftone European pitch row, and European research-musicians can’t distinguish small musical intervals and recognize the appropriate sound pitch systems. In order to derive and fix true results, some devices have been created, which could analyze and draw down the sound pitch direct from a sound recording (Appunn’s Tonometer, 1879 — Seeger’s Melograph, 1951 —1961 and many authors and devices between them). In order to write down the results exactly, famous British scientist Alexander Ellis (1814–1890) proposed using of musical cents (1 octave = 1200 cents, 1 halftone = 100 cents).

Catalogue of traditional melodies or mode structures and some specially measured characteristics of style like pitch row and musical ornamentation, with the indication of performer person and other national and regional attributes, can be further used for comparison of any unknown traditional music records in order to define the performer or his geographical area. A prototype of such system has been elaborated in the 1980th by Russian ethnomusicologist Vladimir Goshovsky (1922–1996). He catalogued examples of Armenian singing folklore by means of electronic computer (Goshovsky 1983). Each example could be described with 80 parameters; this system represented essentially new and more perfective type of catalogue. During the Soviet period (in 1970–1980th), the Uzbek researcher Lev Koval’ studied acoustic parameters of traditional instruments of Central Asia and timbre characteristics of voices of Shashmaqom performers (Koval’ 1988). His work is still relevant now and will be continued in our computer sound analysis.

Some fundamental approaches to computer-aided analysis of audio-signals, which became later useful for musicological investigations, have been described in (Cogan 1985). At present time, computer becomes the main instrument for musical sound investigations. In 2000, the International Society of Music Information Retrieval (ISMIR) has been organized (Downie, Byrd, Crawford 2009). One of directions of ISMIR investigations is “computational ethnomusicology” (Tzanetakis et al. 2007; Oramas, Cornelis 2012). There work also some special scientific groups like COFLA (Computational analysis of Flamenco music); the CompMusic project included investigations on Turkey, China and India music. Micro-deviations from prescribed pitches and durations were analyzed in (Leech-Wilkinson 2009; Devaney, Mandel, Fujinaga 2012) and some other works.

A prevalent part of ISMIR investigations is oriented towards automatic systems developed for searching melodies in a data bank and recognizing of melody or accord sequence for further identification of author. These works suppose that all musical pieces to be analyzed use the 12-halftone pith row with 100-cent steps between stages. (The best result of accord recognizing under these circumstances is near to 80% of correct recognized accords (Mauch 2010)). Only a small part (about 5,5%) of ISMIR investigations deals with analysis of traditional musical cultures (Gedik 2012).

In 1993, a Computer Centre has been organized in the Moscow P. I. Tchaikovsky Conservatory. In 1994, one of the authors of this paper (A. Kharuto) began to develop his computer programmes for different measurements of musical sound — independent from the type of pitch row. Now it is the programme SPAX for Windows (Kharuto, 2005). With the use of this programme (and its earlier DOS-versions) many studies of different traditional singing technique and also of instruments and instrumental music have been fulfilled. There were Tuva throat singing, Peking opera voices, Kalmyk and Korean traditional musical instruments, examples of Azerbaijani, Tajik, Uzbek classical music and Kazakh instrumental music etc.

Aims and methods of sound analysis for ethnomusicology

Professional hearing-out of music sound presumes a specific analysis of its properties. Computer sound analysis must give results which correspond with the musician’s hearing estimations and provide more precise measurements. (For instance, a European ethnomusicologist can distinguish between intervals 70 and 100 cents, but nobody will estimate the exact difference in cents. Such measurement can be fulfilled only with help of special technical tools of special computer programmes for musical sound analysis.) Therefore, one of the main tasks of traditional music analysis is the recovery of entire melody line, which means precise sound pitch extraction and also estimation of duration and intensity (relative loudness) of sound. The sound pitch analysis can be fulfilled with the use of various methods (Gerhard 2003; Cheveignй, Kawahara 2002; Boersma, 2001).

Measurements of spectrum parameters and properties of spectrum elements can give important information about characteristics of singer’s voice — relative power of lower and higher singer’s formants etc. (Bartolomew, 1934; Morozov 2008) and also about singing manner, or specific sound character of an instrument.

Characteristics of performance style are in the limelight both in modern musicology and in ethnomusicology. In oral traditions, performing style and individual interpretation are of specific importance because they form the final result — acoustical text (Yunusova 1995). Usually, descriptions of performance of traditional music contain some colourful, but not exact definitions, which try to portray the style of performance, timbre palette, and also the specific of sound pitch row. However, now it is possible to get more accurate and objective descriptions of these phenomena by using of computer methods.

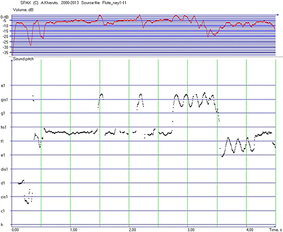
The most informative overview of sound properties during the entire performance represents the dynamical spectrum in form of a ‘sonogram’ (a halftone image in coordinates frequency — time), which is a sequence of ‘momentary’ spectrums calculated within short ‘analysis windows’ (duration 20..50 ms), which slides along time axis with a small time step — for instance, 5, 10 or 20 ms. On this halftone picture, more powerful sound oscillations will be represented with darker points; absence of oscillations corresponds with white space. Dark points build lines with horizontal orientation, which represen overtones.

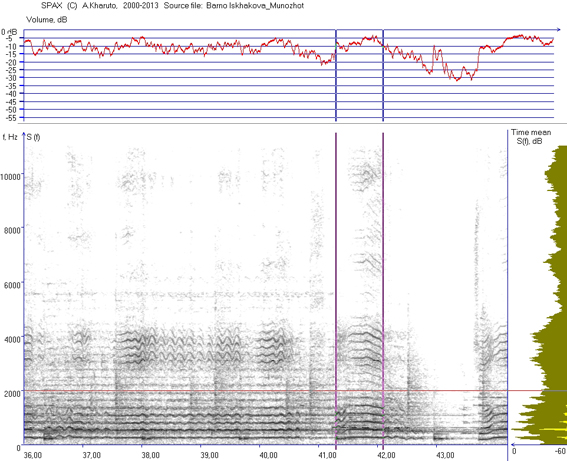
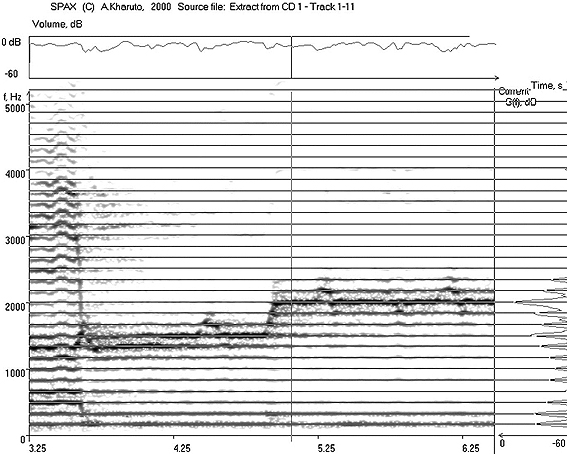
Figure 1 shows an example of sonogram which represents a fragment from composition “Munozhot” performed by famous Tajik women-singer Barno Iskhakova (1927–2001), a great performer of Central Asian classic music Shashmaqom and other classical melodies. One of the authors, V. Yunusova, worked together with her in 1982–1991 in Dushanbe at the Department of Oriental music, which deals with Shashmaqom performers. Her voice had always been a role model for young singers, but her timbre — beautiful, strong, velvet and at the same time with silver sounding — can be described only in words. Computer analysis helps to derive some objective information for description of her unique voice.

Figure 1. Dynamical spectrum (fragment) represented as a sonogram (Barno Iskhakova, Munozhot). On the right border, the time-mean spectrum is shown, calculated for time interval between two given moments (marked with vertical lines). The spectrum part over 2000 Hz (horizontal marker) belongs to high singer’s formant

On the right border, the time-mean spectrum is shown; it has been calculated for the time interval between two given moments (marked with thick vertical lines). These time boundaries have been defined in order to measure mostly the voice and not the instrument sound, which will be represented on sonogram with strong horizontal lines — like shown after t =42 s. (The lack of fragments with a cappella voice sounding is a typical problem of such investigations.) The upper part of spectrum (over 2000 Hz) belongs to high singer’s formant; relative power of this spectrum part in comparison with full power of sound affects the sonority of voice (Bartolomew, 1934).

In order to estimate the voice sonority of B. Iskhako-va, two records have been used, both classical melodies — “Munozhot” (https://www.youtube.com/watch?v=SWnDADNb65I) and “Nowruzi” (recording from personal V. Yunusova’s archive). Computer analysis showed that the high singer’s formant of B. Iskhakova contains about 4..8% of full energy.

Let’s note, that the sonogram calculation is available in many programmes (for instance, well-known Sound Forge, WaveLab, etc.), but these programmes are oriented on common sound editing manipulations and don’t provide such functions as measurement of relative power of high singer’s formant, or power and frequency position of spectrum elements. In SPAX programme, these functions are certainly realized — between many others specific measurements for ethnomusicology investigations.

Frequency positions of overtones will be defined by the main tone frequency (percept as sound pitch — Helmholtz, 1863); increasing of distances between overtones denotes rising of sound pitch. Extracting of melody line is one of most required tasks. For ethnomusicological investigations, the exactness of pitch estimation must be about 4..5 cents, which accords to usual possibilities of human’s hearing. About 10 ‘popular’ methods of estimating the sound pitch have been developed; they apply different mathematical approaches. For example, sound pitch measurement can be based on auto-correlation function of sound oscillations (Boersma, 2001), or calculation of weighted quadratic difference between sound samples with further numerical minimization of supposed period, as in YIN algorithm (Cheveigne, Kawahara, 2002), or cepstrum² calculation method, which proposes two Fourier transforms with logarithmic transformation of spectrum after the first step (this approach nears the cepstrum method to human’s perceiving). As it have been shown in (Kharuto 2015), by using of three ‘basic’ methods listed above, the required accuracy will be achieved under sufficient signal-to-noise ratio (10 dB or more) and suitable form and size of the ‘analysis window’ in time domain; the cepstrum method is more resistant to additional noise or tone. In SPAX programme, all three methods are realized, and the researcher can choose one of them or compare results derived by different methods (usually, they differs in some details).

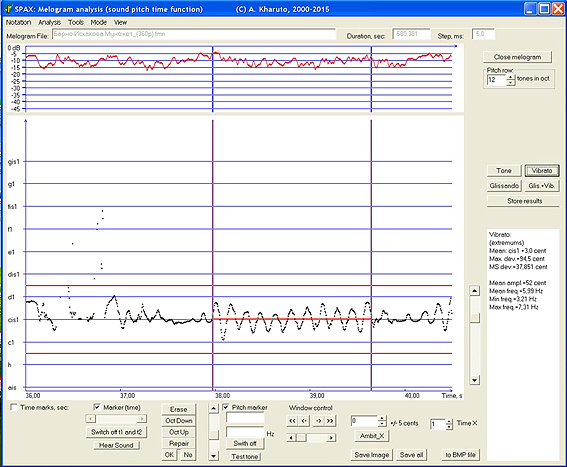
Figure 2 (a screen copy from SPAX programme) represents the melogram — melody graph, calculated for the first half of time fragment shown on figure 1. The time step of sound pitch calculation is 5 ms. \

Figure 2. Melogram of the same phonogram fragment as shown on figure 1. Vertical lines define the time interval where vibrato parameters will be measured (results — in the right field).

Calculation of entire melody line allows to select and measure parameters of melody elements like ‘tones’ (sounds with approximately constant pitch) and glissandos (monotone changing pitch). The wave-like behaviour of melody curve corresponds with vibrato (periodical sound pitch changing), which can be combined with a ‘tone’ or with a glissando (Kharuto 2003, 2004). For instance, measurement of vibrato parameters in SPAX programme for given time interval (vertical lines on figure 2) gives following results (see right text field on figure 2): the mean sound pitch of the tone (from t = 37,97 s to 39,64 s) is equal to cis¹+3 cents (i.e. 3 cents higher then cis¹); maximal pitch deviation from this mean tone value — 94.5 cents, mean-square deviation (effective amplitude) — 37.85 cents; vibrato frequency varies from 3.21 Hz to 7.31 Hz, average value is f = 5.99 Hz. These parameters will be fixed in computer memory and can be analysed for different aims.

For example, investigations of vibrato parameters of some famous academic singers showed that vibrato properties vary during singing in stochastic manner; its statistical parameters are also different from one performance to other one (for the same piece and singer). But, average values of vibrato frequency and amplitude are quite stable for every singer and are rather individual characteristics of the given performer (Kharuto 2006).

(Let’s note, that some other computer programmes, which also can measure the main tone frequency, but are not oriented onto musicological investigations, will be less suitable for such studies because they usually represent results of pitch measurement as frequency in Hertz — and, maybe, with not sufficient accuracy of estimation. Such programmes don’t measure parameters of glissando or vibrato.)

Statistical approach in musical sound analysis

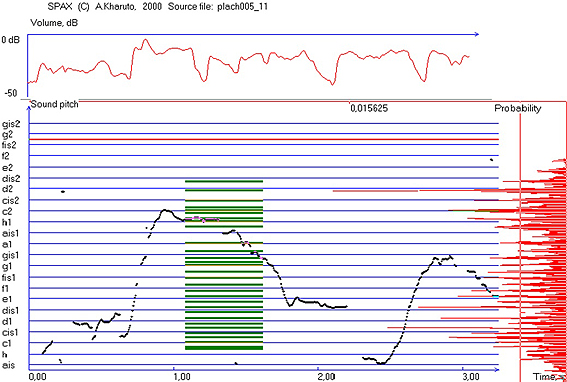
Calculation of statistical distribution of the sound pitch enables to recover the pitch row used by the examined performer, because the stages usually sound remarkable longer (overall) than interim pitches. Such a distribution of sound pitch is shown on the right border on figure 3 (a lamentation example from North of Russia — recording made by D. V. Smirnov, scientific fellow of Moscow P. I. Thaikovsky Conservatory; personal archive of A. Kharuto). The distribution (experimental histogram) contains a set of windows with 5-cent width (in SPAX programme). The horizontal size of every histogram window (bar) is proportional to the overall time of using the appropriate sound pitch. In order to define stages of the pitch row, local maximums of distribution (peaks) will be found and compared with a time threshold T (minimal sounding time) shown on figure 3 as vertical line across the distribution graph. All the peaks which exceed the value T are possible stages of pitch row (Kharuto, 2010). The time T will be defined as the minimum value, which already separates the ‘long enough’ sounding stages (as shown on figure 3). Detected stages are shown as thick lines in the centre.

Figure 3. Statistical distribution of sound pitch (on right border). Vertical line across the distribution graph shows a ‘time threshold’ T: the pitches with longer (than T) sounding will be defined as stages of pitch row. Thick lines in the centre mark detected stages.

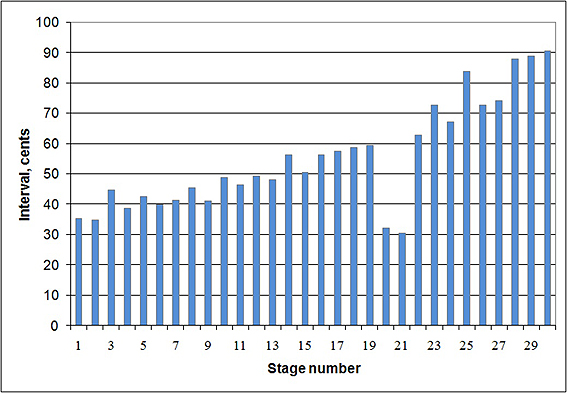
In many folk singing examples, the distribution of sound pitch includes an equidistant structure like European equal tempered pitch row. But, as a rule, the pitch row of folk singing has more than 12 stages in octave — this number varies from 15 to 30 or more (Kharuto, Smirnov 1999; Smirnov, Kharuto 2000). In some other pieces (like shown on figure 3), the pitch row contains linear rising intervals between stages (in this case — from about 35 cents to 90 cents within 1.5 octaves), as shown on figure 4.

Figure 4. Resulting sound pitch row of ‘linear rising’-type: intervals between stages grow from 35 to 90 cents (see also figure 3).

A statistical analysis method like this used A. Gedik in his computer system for study the performances of classical Turkish music (Gedik 2012). The system allows to analyse performer’s acoustical text and to fix it with the national 24-stage notation system. Furthermore, for maqam identification, this programme calculates cross-correlation coefficients between experimental sound pitch distribution and muster-distributions for different maqams, which were firstly derived from a certain number of performances of every maqam. Such statistical approach allowed A. Gedik to analyse and classify phonograms in spite of deviations from ‘prescribed’ text, which are usual in performance of this music.

Some results of computer investigations, fulfilled with SPAX programme

Sound pitch row of Kazakh traditional instruments

Exploring the problem of the specificity of sound in the music of the Turkic peoples, Kazakh researcher Saule Utegalieva proposed a timbre-register sound model, which merged into a single conception tone and pitch of the sound (Utegalieva 2013). To determine the exact parameters of pitch rows in traditional Kazakh music performance — in addition to the linear measurement of instruments — computer analysis has been used. It has been shown, these pitch rows differ very much from European 12-halftone pitch row and may contain musical intervals of natural and also of Pythagorean system. This computer investigation was carried out by S. Utegaliyeva & A. Kharuto with the use of SPAX programme; some results were published in (Utegalieva, Kharuto, 2013a, 2013b). In these studies, an important problem was the application of necessary ‘ruler’ which represents the sound pitch system of the examined music. In due time, one of authors (V. Yunusova) advised to replace the designation of stages in European equal-tempered system onto other — Pythagorean and natural pitch row. These systems described traditional Kazakh instrumental music more adequate.

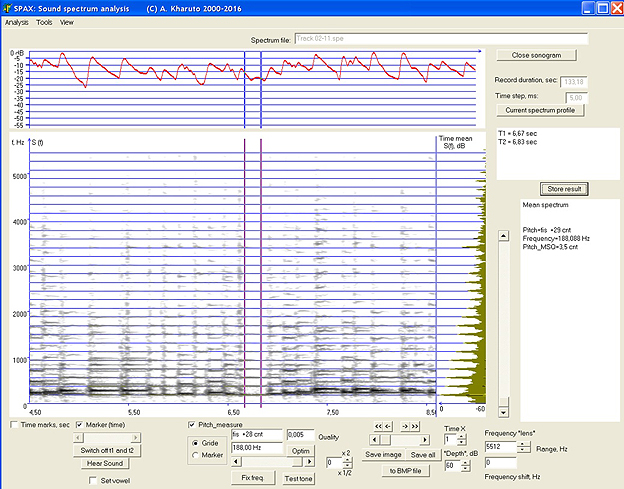
The analysis methods for extracting of melody listed above work only with monophonic sounds (only one string, only one human’s voice etc.), but Kazakh national instruments like dombra have more strings. Because of this, we did not use automatic mode of sound pitch estimation in SPAX programme. Instead of this, a half-automatic mode has been used: a ‘theoretical’ system of harmonics with main tone frequency fr was positioned over the calculated sonogram, and the parameter fr has been varied manually in order to achieve the best coincidence between experimental and ‘theoretical’ harmonics system. Such ‘best’ matching is presented on figure 5. After manual adjustment of main tone frequency fr , an automatic algorithm was applied, which minimized the disparity of ‘theoretical’ and experimental harmonics with accuracy about .05 Hz.

On figure 5, the selected sound is monophonic; sounds after t = 6.7 s were produced by two strings and contain two overtone systems. For such sounds, the same procedure has been applied many times: firstly the ‘best matching’ was achieved for one overtone system, and then — for other overtone row, and so on. In this way, multi-voice sounds can be examined with SPAX programme.

Figure 5. Sonogram of Kazakh dombra (fragment: recording from personal archive of S. Utegalieva). Thin horizontal lines are the ‘theoretical’ harmonics after manual adjustment of main tone frequency f. The two vertical lines (set by researcher) are time bounds for sound pitch measurement. Right field shows time-mean spectrum of the selected sound.

The real value of main tone frequency of dombra is variable on the duration of every sound because of some noise components and also technique of sound production. In this situation, a statistical approach was applied: instead of one-point pitch estimation, time-mean value of sound pitch was measured, and also mean-square deviation of momentary sound pitches from this mean value was calculated on sound duration. For the given sound, the pitch was fis +29 cents (fr = 188.09 Hz), pitch mean-square deviation = 3.5 cents. The mean-square deviation, measured for about 40 different sounds, does not exceed 5.5 cents. Because of this, intervals could be measured with the accuracy of about 5.5+5.5 = 11 cents; therefore, we could reliably distinguish between intervals like 25 cents, 50 cents and bigger. Some results of measurements are shown in table 1. Most intervals (68.5%) were close to 25 cents or multiple of it (25x). About 11% of intervals are near to ‘European’ pitch row (multiple of 100 cents — 100x).

Table 1.Results of pitch row measurement for Kazakh dombra music

Interval, cent	Number of intervals	Number of intervals in %
25x	26	68.5
50	0	0
100x	11	29
150	1	2.6
Total	38	100

This computer investigation allowed to specify the sound pitch system and performance techniques of Kazakh traditional instrument. The book written by S. Utegalieva includes many other results of SPAX-measurements of Kazakh instrument- and performing style properties (Utegalieva 2013); some results have been published in (Utegalieva 2016).

Tuva throat singing

In the investigation of Tuva throat singing, some significant properties of this kind of singing were discovered, and a new model of two-voice sound producing was suggested (Kharuto 2008; Kharuto, Karelina 2008). It was shown that the ‘presence of two independent mechanisms’ of producing the well-known ‘two voices’ during vocalize part will not be proved on the base of the sonograms, because it contain always only one overtone system with burdon frequency as the main tone. An example of such sonogram is shown of fig. 6 (sygyt style, beginning of vocalize part). On the right border is shown a momentary spectrum for the time moment t=5 s (marked with vertical line across the sonogram). The ‘two-voice’ perception can be explained through the presence of two formants (darker overtone lines) — the lower one (under 500 Hz) and the second formant, which varies its position in the area from approximately 1200 Hz (d³) to 2500 Hz (d⁴).

Fig. 6. Sonogram of Tuva throat singing (sygyt style, vocalize part begins at 3.5 s)

The presence of a second ‘independent’ sound source would produce any other system of harmonics like a second string. But indeed, these harmonics coincide with the spectrum components of the first source. This fact has been explained through a new model of sound producing and proved in computer simulation (Kharuto 2008). The model assumed that the Ferrein’s cords control vestibular cords, blocking the expired air stream with a certain rhythm (main tone frequency f₁). The vestibular cords (which are positioned after the Ferrein’s cords, nearer to the ‘output’) answer every air pressure pulse with an aerodynamic whistling on frequencies 2..4 kHz. As result, at the ‘output’ of vocal tract, the sequence of pulses will be formed with the period of oscillations of Ferrein’s cords, and the pulses are ‘filled’ with high frequency oscillations produced by vestibular cords. The spectrum of such oscillations includes only harmonics of f₁ (this fact is known in the theory of radio-technics) — exactly this spectrum form has the khoomei sound.

The described model explains the building of very wide spectrum, which contains only harmonics of burdon tone. Using this ‘source spectrum’, the performer can form a wide-band spectrum for recitative part or a ‘multi-band’ spectrum with two or more formants — for vocalize part. The only ‘material’ for sound producing in this kind of singing are harmonics of burdon tone; because of this specific, vocalize melodies can be based only on natural pitch row (Kharuto, Karelina 2008; Karelina 2009).

Historical pitch row trends in Mugham and Maqom performance

On material of classical music of Transcaucasia and Central Asia (Mugham, Maqom), the authors studied (among other problems) changes in the system of modus and in musicians’ hearing of different performers generations. We revealed prevalence of microtones in performance of traditional musicians of elder generation in comparison with musicians trained in conservatories (Yunusova, Kharuto 2014, 2015, 2016). Specific features of performing style were shown already during measurement of frets positions of the Azerbaijani plectrum chordophone — Tar and Tajik plectrum chordophone Tanbur (tanbour).

Both instruments which have been analysed are the main instruments in traditional classical music of Middle East. On the basis of Azerbaijani tar and Central Asian tanbur, on which in the Middle Ages the theory of classical music — Mugham and Maqom was formed. Both instruments are plector chordophones, they have: tar – 11 strings (including two pairs of melodic strings), tanbur – 3-strings and a lot of fixed frets on the fingerboard. The first of them is well-known from the Middle Ages and uses a 17-stage pitch row with not even intervals between stages. The second one was firstly tuned to the ranks of the same 17-stage, but in the last century it’s tuning became near to 12-steps diatonic system. Therefore, a tanbur owned by elder musicians can contain more frets. Let’s note, that a 17-step per octave pitch row can’t be accurate notated in European system because it contains intervals less than 1/2 tone. Computer sound analysis and graphical representation of melograms allow to estimate and fix the sound pitch row more adequate.

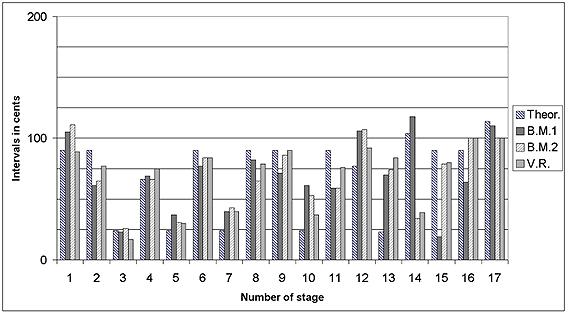
In order to make comparison, there were chosen instruments (Tar) of famous Azerbaijani musician Bakhram Mansurov (1911–1985) and of Mansurov’s former pupil V. Rahimov (Yunusova, Kharuto 2015). B. Mansurov was a great connoisseur of Mugham art, People’s Artist of Azerbaijan; Valeh Rahimov is now Honored Artist of Azerbaijan. Comparison was made between measurement results for instruments of musicians B. Mansurov’s school, also two of his personal instruments. (Linear measurements were executed by V. Yunusova in the early1980th.) The results have been compared with the theoretical 17-degrees scale, used in the Azerbaijani Mughams. For all instruments, individual divergences were also fixed. However, they weren’t very big because musicians of one and the same school follow similar acoustical ideals. Results of these measurements are shown on figure 7.

Figure 7. Theoretical 17-stage pitch row (Theor.), two pitch rows of B. Mansurov’s tars (B.M.1, B.M.2) and the pitch row of V. Ragimov’s (V.R.) tar (all laboratory measurements made on ‘silent’ instruments)

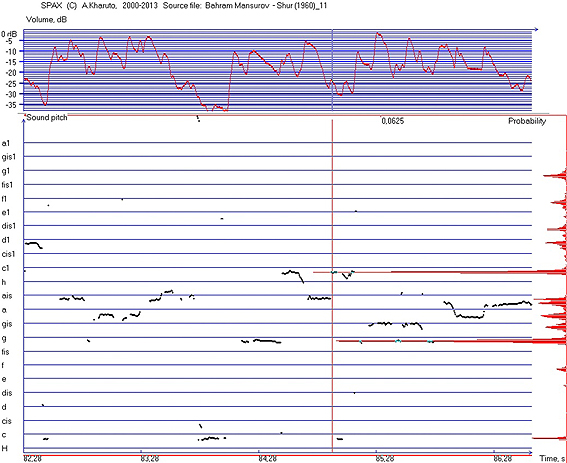
The study pitch rows characteristic for elder and younger generation of performers was based on experimental analysis of sound with the help of computer programme SPAX. For sound pitch measurement, the cepstrum method will be used. The SPAX programme does not follow different ‘voices’ separately, but the cepstrum method fixes the pitch of most powerful sound at every time moment. As result, the ‘summary’ sound pitch row can be estimated, which includes pitches of different sounding strings. Figure 8 shows the sound pitch histogram (at the right border) calculated for the whole phonogram of B. Mansurov’s Shur (Mansurov 1968):

Figure 8. Fragment of melogram of Shur mugham (B. Mansurov) and the histogram of sound pitch (at the right side; probability rises from right to left)

The pitch row was estimated by using of sounding time threshold, as described above. But in some cases, programme will fix pairs of adjacent ‘stages’ with very small pitch difference; this may be accidentally variants of one ‘true’ stage. In order to eliminate such effects, in SPAX programme a second variable parameter will be used —Q_min, the ‘minimal allowed’ distance between pitch row stages. If the distance between two stages is less than Q_min, the programme will substitute the pair of ‘stages’ through one stage with a weighed mean value of sound pitch and summarize its sounding times. For different values of Q_min, the number of fixed stages N will vary. Until Q_min is lower than the real difference between stages, N will retain a constant value. After increasing Q_min over the any real pitch difference, two or more of adjacent stages will be substituted through weighed mean values, and the number N will decrease. In order to define the needed T and Q_min, in SPAX programme a variation-search of both parameters will be fulfilled. T varies approximately from .02 T_max to .2 T_max , where T_max is overall duration of the most long sounding stage (near c1 on figure 8). For a minimum T value, which already separates the ‘long enough’ sounding stages, the Q_minvalue will be defined. For this aim, the beginning of first diapason of Q values, where N ≈ const, will be found and a value Q_min>Q as ‘true’ accepted.

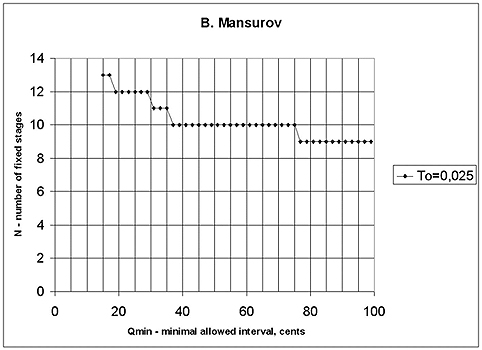
For B. Mansurov’s phonogram, this procedure will be illustrated on figure 9, which shows the number of fixed stages as a function of Q_min. In this case, N is constant (N=12) for intervals Q_minfrom 20 to 30 cents and T = .025 T_max. This ‘area of stability’ for some values of Q_min indicates the minimal interval between stages by B. Mansurov — about 20 cents. According to this estimation and setting Q_min=20 cents, we get a list of stages and intervals between them for B. Mansurov’s performance, shown in graphical form on figure 10.

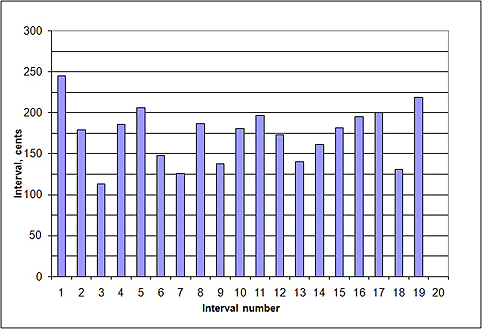
Figure 9. Diagram for number of fixed stages (N) as a function of minimal allowed interval between them (Q_min) for B. Mansurov (1960th). T = .025 T_max Figure 10. Pitch row of B. Mansurov: consecutive intervals

Because of limited accuracy of sound pitch estimation, the intervals can be measured with possible errors of about 10 cents. Taking into account this value, one can see that many intervals on Figure 10 are approximately equal to 25 cents (#5, #8), to cents (#3, #4), or to 175 cents (#7); other 6 intervals are ‘European-like’ — near to 100 cents (#2, #9) or 200 cents (#1, #6, #10, #11). The measurement procedures described above have been fulfilled also for phonograms other musicians.

The plectrum chordophone tanbur, belonging to the great Tajik musician Fazliddin Shakhobov (1911–1974), was measured in acoustic laboratory of the Moscow conservatory in due time. This tanbur had on the neck 19 main frets (bastaparda), which were fasten by an imposing method on the neck, and some additional pastes (4-6 hasparda; their measurements weren’t made). Results of this measurement (Abdukarimov 1997, P.12) is represented in the Table 2.

Table 2. Fazliddin Shakhobov’s tanbur frets (1 line – fret number; 2 – interval in cents)

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
0	245	424	537	723	929	1077	1203	1390	1528	1709	1906	2079	2219	2380	2562	2757	2957	3088	3307

 

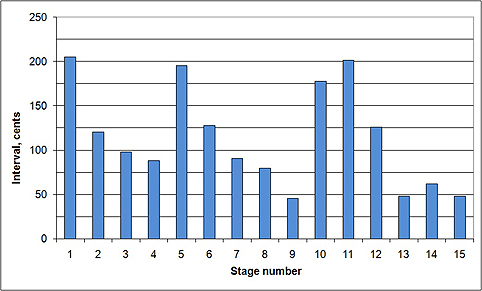
The representation of the measurements of a Fazliddin Shalhoob’s tanbur as diagram is shown on figure 11. Contemporary musician Murat Eshankulov was playing (in 2013) the classical melody Samoi-Dugoh on the same instrument, and we analyzed his actual pitch row; results are shown on figure 12.

Figure 11. Diagram of pitch row intervals of Fazliddin Shakhobov’s tanbur

M. Eshankulov got this instrument in the 1980th; he reduced the number of frets from 19 to 14 in according to his acoustical ideal and experience. His musical hearing was formed under influence of conservatory, where the musician studied not only traditional, but also European classical music. As result, he became focusing on wider intervals and did not need some of frets on tanbur which used F. Shalhoobov, a musician of elder generation. M. Eshankulov wasn’t a pupil of F. Shakhobov, but he studied classical music of Central Asia under the leadership of old masters — Nisan Shaulov (1925–2002) and Nerya Aminov (1916–1996), who worked together with F. Shakhobov in due time (maqoms records in their performance are in the personal archive of V. Yunusova).

Figure 12. Pitch row measurement of Murat Eshankulov’s playing (the classic melody Samoi-Dugoh (recording from personal archives of V. Yunusova and A. Kharuto).

Comparing the silent and sounding instrument (which became possible only with development of computer methods), we get notable distinctions which are always present by string instruments with fixed frets. They show that musicians possess individual hearing (that can be treated also as specific of individual performing style), and frets of the instrument carry out a role of peculiar ruler by which the musician is guided. On tanbur, owing to features of this instrument, deviations can reach half-tone and more. The famous Uzbek scientist Fayzula Karomatov noted that though tanbur has a diatonic scale (unlike other Uzbek string and plucked instruments), because of high over fret-board located strings — and thick frets (bastaparda) — “it is possible to change sound pitch within bounds of half-tone, if pressing a string by various force. This technique produces on tanbur neutral intervals and chromatic half-tones” (Karomatov, 1972. P. 135). These differences assign an interesting task for scientist, and objective decision is impossible without exact computer measurements of the sound.

The results of comparative analysis of intervals in Maqom and Mugham performed by traditional musicians of elder generation and their pupils is represented in Table 3. Let’s note that the measured intervals does not match exactly with 25-, 50-, 75-, 100- and other ‘round’ intervals; we just classify the real values to intervals ‘like 25x — cents interval’ (it means near to 25 cents, to 75 cents, and also to 125, 175 cents and so on) or ‘like 50x — cents interval’, which denotes all the intervals near to 50 cents, to 150, 250 cents and so on, etc. The ‘Euporean-row-like’ intervals (100x&200x) include near-to-100-cents, near-to-200-, -300-cents and so on intervals. Because the accuracy of interval measurement is about 10..11 cents, all the intervals inside of this diapason are included in the same ‘class’ around the centre values.

Table 3. Results of pitch row measurement for two generations of performers

Source phonogram	Number of detected intervals	Number of 25x-int.	Percent of 25x-int.	Number of 50x-int.	Percent of 50x-int.	Number of 100x or 200x cent-int.	Percent of 100x or 200x-cent int.
B. Mansurov (1960-th, tar)	11	6	54,5	—	—	5	45,5
V. Rahimov (1981, tar)	15	5	33.3	6	40	4	26.7
V. Rahimov (2012, tar)	20	6	30	7	35	7	35
N. Aminov (1960-th, tanbur)	12	4	33.3	5	41.7	3	25
M. Eshankoulov (2013, tanbur)	15	4	26.7	4	26.7	6	40

 

Table 3 shows some historical changes in the performing style of classical music during last 50 years, which can be explained through conservatory education of new generation of musicians. The influence of European music with its 12-halftone pitch row provokes increasing of using of 100- and 200-cent intervals and reducing of micro-intervals like 25-cent. Similar results have been derived for two regional tradition of classic music – the Azerbaijani Mugham and Tajik Maqom.

In comparison with instruments with fixed frets (as tanbur or tar), study of wind instruments shows much more flexibility of sound pitch variations; computer analysis allow to measure exact parameters of it.

Iran flute Ney

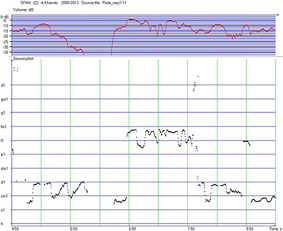
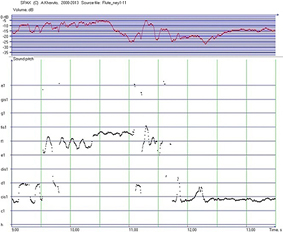
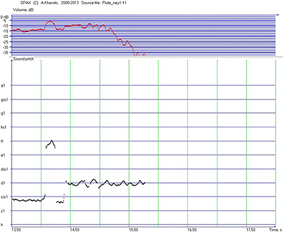
Sound specificity of many Eastern instruments is closely linked with the use of large amount of musical ornamentation: vibrato, glissando, and combinations thereof, etc. Admission ornament is a way to demonstrate the tone. This phenomenon was called by V. Yunusova ‘ornamental articulation’ (Yunusova 1995). An Iranian Ney flute phonogram gives an example of this kind of sounding, which is visible on melogram after its computer analysis (figure 13). In comparison with instruments which have fixed frets (as tanbur or tar) this wind instrument has more variable melody line. For example, the first vibrato, which begins at t1=2.77 s and ends at t₂=3.30 s, has the mean tone gis¹-5.8 cents, mean vibrato frequency — 6.38 Hz, vibrato amplitude about 38 cents. Next vibrato between t₁=3.64 s and t₂=4.07 s has the mean tone f¹-28.4 cents and frequency 6.12 Hz with amplitude 49 cents.

 

Figure 13. Flute Ney melogram (Iran: personal archive of V. Yunusova)

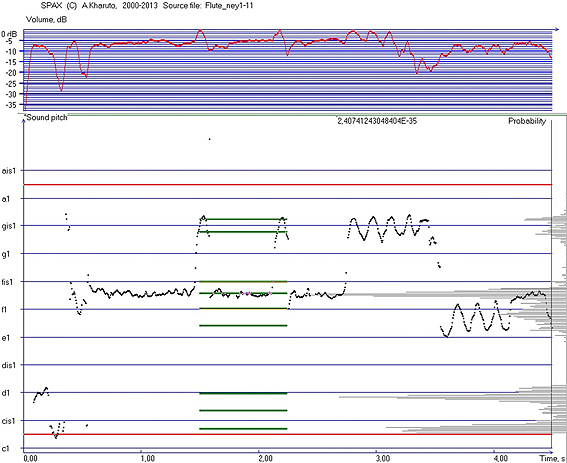
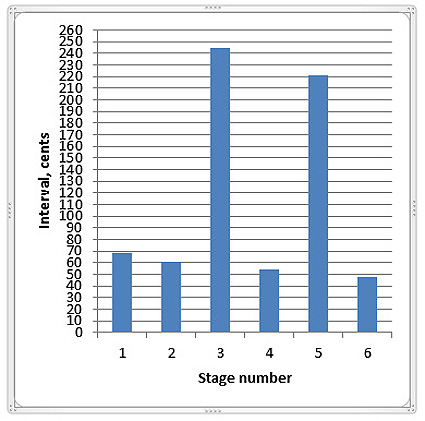
Statistical distribution of sound pitch (for a fragment duration 16 s) is shown on figure 14. For some appropriate analysis parameters (time threshold level 8%, minimal ‘allowed’ stage interval 40 cents) the detected pitch row will contain 8 stages, as shown on figure 14 (thick horizontal lines in the centre). On this picture, the two upper ‘stages’ are maximal and minimal pitch values of vibrato (time fragment 2.8..3.5 s). The mean tone of this vibrato is gis¹-5.8 cents. Also the ‘stages’ #4 and #5 (from beneath) are bounds of vibrato; they can be substituted through a tone f¹-28.4 cents. The pitch row (after these operations) will contain 6 stages, as it is represented on figure 15 (the lower stage is 66.4 cents higher than c¹).

Figure 14. Statistical sound pitch distribution (right) for the flute Ney melogram (histogram estimated on entire duration). Thick lines in the centre show the detected pitch row stages

Figure 15. Pitch row intervals in the Ney flute performance

Conclusion

Application of computer-aid research in ethnomusicology expands its methods. Computer analysis of traditional music of Asia is a scientific direction inside the Computer Ethnomusicology. Methods of computer analysis are relatively widespread in modern music and ethnoorganology, where they allow to explore changes in musical instruments structure made under the influence of new sound ideals of last generations of musicians. In less degree these methods are applied in research of performing style of musicians, however improvement of mathematical methods and appropriate computer programmes may lead to remarkable prospects in this direction.

---

1. Some part of this material was published in (Yunusova, Kharuto 2016).

2. The name of CEPS-TRUM method uses the same letters as ‘spec-trum’, but partially in reverse order.

References

Abdukarimov, Murodullo. 1997 “Tanbur, Sato and Setor in musical tradition of Uzbekistan and Tajikistan”. PhD. Thesis. Tashkent.

Bartolomew, Wilmer Tillett. A Physical Definition of “Good Voice Quality” in the Male Voice// Journal of Acoustic Society, 1934, N 6, p.25–33.

Boersma, Paul. 2001“PRAAT, a system for doing phonetics by computer”. Glot International 5 (9/10): 341–345.

Cheveigné, Alain de; Kawahara, Hideki. 2002 “YIN, a fundamental frequency estimator for speech and music” Journal of Acoustic Society of America.111 (4): 1917–1930.

Cogan, Robert. 1985 New images of musical sound. Cambridge, Massachusetts: Harvard University Press.

Devaney, Johanna; Mandel Michael; Fujinaga, Ichiro. 2012 “A study of intonation in three-part singing using the automatic music performance. Analysis and Comparison Toolkit (AMPACT)”. Proceedings of the 13. International Conference on Music Information Retrieval (ISMIR 2012): 511–516.

Downie, J. Stephen; Byrd, Donald; Crawford, Tim. 2009. “Ten Years of ISMIR: Reflections on Challenges and Opportunities” Proc. of ISMIR: 13–18.

Gedik, Ali Cenk. 2012 “Automatic Transcription of Traditional Turkish Art Music Recordings: A Computational Ethnomusicology Approach”. A Thesis Submitted to the Graduate School of Engineering and Sciences of İzmir Institute of Technology in Partial Fulfillment of the Requirements for the Degree of Doctor Of Philosophy in Electronics and Communication Engineering, İZMİR.

Gerhard, David. 2003 “Pitch Extraction and Fundamental Frequency: History and Current Techniques” Technical Report TR-CS 2003-06, November, Department of Computer Science, University of Regina. Regina, Saskatchewan, Canada.

Goshovsky, Vladimir. 1983 To typology of the Armenian song of "Gorani". (Experience of research by means of the Computer) Yerevan: Academy of Sciences Armenian. Soviet Socialist Republic, Hsu, Chao-Ling; Chen, Liang-Yu; Jang, Jyh-Shing Roger ; Li, Hsing-Ji. 2009 “Singing pitch extraction from monaural Polyphonic songs by contextual audio Modeling and singing harmonic enhancement” Proc. of ISMIR 2009: 201–206.

Helmholtz, Hermann Ludwig Ferdinand von 1863 Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, Vieweg, Braunschweig 1863, Nachdruck: Minerva-Verlag, Frankfurt/Main 1981, ISBN 3-8102-0715-2. (On the Sensations of Tone as a Physiological Basis for the Theory of Music. Third Edition of English Translation, based on Fourth German Edition of 1877, By Hermann von Helmholtz, Alexander John Ellis, Published by Longmans, Green, 1895, 576 pages.)

Karelina, Ekaterina History of Tuva music from the downfall of Tsin dynasty until to our time. An investigation Moscow, Moscow P. I. Tchaikovsky conservatory, Composer publishing house.

Karomatov, Faizulla 1972 Uzbek instrumental music. Tashkent: Publishing house of literature and arts named after Gafur Gulyam.

Kharuto, Alexander; Smirnov, Dmitry. 1999 “Using of computer analysis in investigations of folk music”Proc. of International scientific conference in memory of A.V. Rudneva: Music of oral tradition. Moscow P. I. Tchaikovsky Conservatory: 335–340 (in Russian).

Kharuto, Alexander. 2000. “Computer Transcription of Phonograms of Folk Singing” In: Leonid Dorfman, Colin Martindale, Vladimir Petrov, Paul Mahotka, Gerald Kupchik (Eds.). Creativity in Art — Art of Creativity [Tvorchestvo v iskusstve — iskusstvotvorchestva]. Moscow, Nauka; Smysl:325–336 (in Russian).

Kharuto, Alexander. 2003 “Folk music sound: Methods and results of computer analysis”. Current Trends in Russian Approaches to Art and Culture. Bulletin of Psychology and the Arts, Society for Psychology of Aesthetics, Creativity, and Culture.3: 35–37.

Kharuto, Alexander. 2004 “About Elementary Musical Sounds Used in Vocal Performance (Theoretical and Empirical Study)”. In Joao Pedro Frois, Pedro Andrade Marques, Jose Frederico Marques (Eds.) Proceedings of the XVII Congress of the Association of the Empirical Aesthetics. C.Gulbenkian Foundation, Lisbon, September 13-16 IAEA, Lisboa: 152–156.

Kharuto, Alexander. 2005 Programme SPAX for Windows. Reg. #2005612875 of Federal Institute of Industrial Property of Russia. A demo-version is available on http://www.kharuto.ru/SPAX-demo

Kharuto, Alexander. 2006 “Computer analysis of vibrato properties in academic vocal performance”. In: Hana Gottesdiener, Jean-Christofe Vilatte (Eds.) Culture and Communication. Proc. of the XIX Congress of IAEA.Univ.de Avignon, pp. 226 – 229.

Kharuto, Alexander. 2007 “Computer Sound Analysis in Musicology: Its Goals, Methods, and Results”. In Leonid Dorfman, Colin Martindale, Vladimir Petrov (Eds.) Aesthetics and Innovation . Cambridge Scholars Publishing: 305–322.

Kharuto, Alexander. 2008 “Tuva throat singing: forming of many voices from a ‘single-voice’ spectrum (model of sound production and perception)”. Abstracts of V International symposium on khoomei (throat-singing) — cultural phenomenon of the peoples of Central Asia. UNESCO National Committee of Tuva Republic, International Scientific Center ‘Khoomei’, Kyzyl, Russian Federation:134–142.

Kharuto, Alexander. 2009 “Computer Sound Analysis in Musicology and Music Teaching” Muzykalnaya akademiya (Musical Academy), (4): 77–83 (in Russian).

Kharuto, Alexander. 2010 “Computer Analysis of Sound Pitch Row made on Phonogram” Muzykalnaya akademiya (Musical Academy) (3) 83–89 (in Russian).

Kharuto, Alexander. 2011. Analysis of Sound Pitch for Investigations in Professional- and Folk Singing. Measurement of Interpretation. Computer-aid Analysis of phonograms in cross-examination of disciplines. Sound and conception, v. 4. Heinz von Loeschand Stefan Weinzierl (Eds.). Mainz: 173–191 (in German).

Kharuto, Alexander 2015 Computer sound analysis in musical science. Moscow P. I. Tchaikovsky Conservatory, 448 P. (in Russian).

Kharuto, Alexander and Karelina, Ekaterina 2008 “About musical and acoustical properties of Tuva throat singing.” Musical Academy (Muzykalnaya Akademiya), (4): 108–113. (In Russian).

Koval', Lev 1988 Problems of training of musical hearing (based on intonation system of Uzbek monody). Problems of professional teaching of musicians. Tashkent: Publishing house of literature and arts named after Gafur Gulyam, 1988: 102–108.

Leech-Wilkinson, Daniel 2009 The Changing Sound of Music: Approaches to Studying Recorded Musical Performance. Published online, London, CHARM.

Mauch, Matthias 2010 “Automatic Chord Transcription from Audio Using Computational Models of Musical Context”. Thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy of the University of London. School of Electronic Engineering and Computer Science Queen Mary, University of London. 169 p.

Mansurov, Bahram 1968 Азербайджанские народные мелодии. “Шур” [Azerbaijani folk tunes]. Performed by Bahram Mansurov (tar), ГОСТ5289-68 33Д-14928 Melodiya. Moscow LP Record.

Morozov, Vladimir 2008 Art of resonance singing. Basis of resonance theory and technique. /The Moscow P. I. Thaikovsky Conservatory, Institute of Psychology of Russian Academy of Science, Moscow, 2008. 592 p. (in Russian).

Oramas, Sergio;Cornelis, Olmo. 2012 “Past, Present and Future in Ethnomusicology: the Сomputational Challenge” Proc. of ISMIR-2012, 2p., dem.

Smirnov, Dmitry; Kharuto, Alexander. 2000“ Non-linear sound pitch row in musical folklore: common consistent pattern and individuality”. Languages of sci¬ence — languages of art In Zoya Zu¬ravleva, Vladimir Kopzic, Galina Rezni¬chenko (Eds.). Progress-Traditsiya: 347–352 (in Russian).

Tzanetakis, George; Kapur, Ajay; Schloss, W. Andrew; Wright, Mathew. 2007 “Computational ethnomusicology”. Journal of Interdisciplinary Music Studies 1 (2): 124.

Utegalieva,Saule. 2013 Sound World of Music Of the Turkic Peoples: theory, history, practice. Moscow, “Compozitor” Publishing House (in Russian).

Utegalieva,Saule and Kharuto, Alexander 2013а. “Computer Analysis of Traditional Pitch Row of Kazakh Dombra made on a Fragment from D. Nurpeisova’sKui ‘Enbek epi’”. Musicology.(8): 28–39 (in Russian).

Utegalieva,Saule and Kharuto, Alexander. 2013b “Computer investigations of pitch rows of Kazakh kyl-kobyz”.Musicology, (12):38–45 (in Russian).

Utegalieva,Saule 2016 “A Computer-base Study of Scales on the Kazakh Dombra and Kyl-Kobyz.” //Yearbook for Traditional Music (Intarnational Councilfor Traditional Music. UNESCO) – 2016. – Vol. 48, pp. 146–166.

Yunusova, Violetta. 1995 “Creative process in Classical music of Orient”. Doctor of Art Dissertation. Moscow. Moscow state P.I. Tchaikovsky conservatory.

Yunusova, Violetta and Kharuto, Alexander. 2014 “Objective Analysis of Performance Style Parameters (On The Material Of Classical Music Of The East)” Proc. of the 24th National Scientific Symposium with International Participations “Metrology and Metrology Assurance”, Sept. 7–11, Sozopol, Bulgaria: 96–100.

Yunusova, Violetta and Kharuto, Alexander. 2015 “Computer Analysis of Style Parameters in Traditional Culture Performance (on Material of Classical Eastern Music” Musical Academy), (1): 143–147 (in Russian).

Yunusova, Violetta and Kharuto, Alexander. 2016 “Computer Sound Analisis of Traditional Music of Transcaucasia and Central Asia” //Yearbook for Traditional Music (Intarnational Councilfor Traditional Music. UNESCO) – 2016. – Vol. 48. – pp.136-145.

Glossary of terms

Bastaparda – 14-19 main frets on the neck of Tajik-Uzbek plektrum chordophone Tanbur are important for modal features of the executed melody.

Hasparda – additional paste (4-6 ) of Tajik-Uzbek plectrum chordophone Tanbur are located on a neck and on the top of sounding–board of instrument.

Khoomei – general name of different styles of the Tuva throat singing in which besides the main tone still the overtones and aerodynamic whistle making impression of the second and even the third voice are heard.

Maqam– 1) general name of modes of music of the Near and Middle East; 2) the genre form of classical music based on the maqam modes, the multi parts vocal-instrumental cycle.

Maqom–Central Asian version of maqam.

Mugham–Azerbaijani version of maqam.

Munozhot–the classical Uzbek and Tajik melody.

Ney – a cross flute, is widespread in Central Asia, China, in the Near and Middle East.

Nowruzi–the classical Uzbek and Tajik melody.

Samoi-Dugoh–the classical Uzbek and Tajik melody.

Shashmaqom–(literally six maqom) the multi parts vocal-instrumental cycle from six (in the Middle Ages – 12) Maqoms: Buzruk, Rost, Navo, Dugoh, Segoh, Irok.

Sygyt–(literally whistle) one of the five main styles of the Tuva throat singing, characterized by the whistling additional sound above the main tone.

Tanbur – in this case Tajik-Uzbek plectrum chordophone, the main instrument for the theory of classical music of Central Asia – maqom.

Tar – in this case Azerbaijani plectrum chordophone, the main instrument for the theory of classical music Azerbaijani mugham.